Today we’re going to build our own functions to simulate movement on landscape. This may be a slow process at first, but once you get the hang of building and using functions, you’ll see how powerful they can be. Ultimately, we’ll actually implement the functions we develop here on a landscape that we will also be simulating (later in the day). Throughout these exercises, I am going to use a code_folding option that will hide the code in the blocks below (at least in the HTML output) until you click on it to expand. I have chosen to do this because I will have a few challenges for you to try as we develop some of these functions. I don’t want to give away all the answers in case you want to try to solve them independently, so they will be hidden until you choose to see them!
Let’s begin by breaking down the movement process as we see it recorded by GPS or other telemetry devices. The two things we need to define a step are a step length and a turning angle. These are the two basic measures that we extract at the start of many analysis methods because these are the fundamental units of our analyses. We’ll say, for now, that our starting point on a Euclidean plane is the origin (0,0) and the animal is able to move in any direction. Essentially, our problem is very simple: we want to choose a step length and turning angle and return the position of the individual when they are next recorded.
We can very easily use R’s built-in capabilities of selecting a random number from a distribution to select a step length and turning angle for our next point. Our choice of distributions will be the most important factor here, but we are going to work from an extremely basic starting point and then move into some more complex (and more accurate) distributions. For our step lengths, lets select from a normal distribution (base::rnorm) whose mean is 500 meters and who has a standard deviation of 100 meters. If we wanted to see what a series of these random step lengths would look like, we could easily plot a histogram of, say, 10000 draws:
hist(rnorm(n=10000, mean=500, sd=100))
Alright, it may not reflect and empirical movement path precisely, but it will do the job. Now lets use a uniform distribution to represent the turning angle. This angle can range from -pi to pi (-3.14 to 3.14), and if we take a look at 10000 draws from this uniform distribution, this is what it will look like:
pi = 3.141593
hist(runif(n=10000, min=-pi, max=pi))
This suggests that our animal is completely unaffected by the previous direction it came from (i.e., its movements do not exhibit persistence in a given direction), so it is not entirely accurate, but it will do for now.
There are our two values, ready to be selected at random from our pre-defined distributions. But how do they turn into a new point? Well, trigonometry is how!
If we think back to high school, you’ll perhaps recall that, with an angle and the length of the hypotenuse, we can solve for every other aspect of a right triangle. All movements can be reduced to right triangles, and what we really want are the lengths of the adjacent and opposite sides because those represent the changes in the x and y coordinates. All we need to simulate our own movement paths are these two coordinates.
So what does it look like to use trigonometry in R? Well, its quite straightforward. In order to extract the change in the y coordinate associated with a turning angle and step length, we want to solve for the opposite side. That means we should use sine with our known angle and our hypotenuse (opposite = sin(angle) * hypotenuse). To solve for the change in the x coordinate, we want to solve for the adjacent side, which requires the use of cosine with our known angle and the hypotenuse (adjacent = cos(angle) * hypotenuse).
That is pretty easy. Lets build a function now in which we begin with the starting point, which we will refer to as xy, the step length (step), and turning angle (heading), and then return a small data frame that records the new x and y coordinates as well as the inputs that brought us there.
movement <- function(xy, step, heading) {
#First we need to define pi
pi = 3.141593
#Then we split the starting point into an x_init and y_init
x_init <- xy[1,1]
y_init <- xy[1,2]
#Here we translate the negative pi values into positive values
#The headings now range from 0 to 2*pi
if (heading < 0) {
heading <- abs(heading) + pi
}
#Using this heading, and our sin function, we can solve for the change in y
#Then we want to create a new value where we alter the starting y value
y_change <- sin(heading)*step
y_new <- y_init + y_change
#The use cosine to determine the movement in x direction
x_change <- cos(heading)*step
x_new <- x_init + x_change
#Finally, we create a data frame and save our new coordinates
move.temp <- as.data.frame(matrix(0,1,4))
move.temp[1,1] <- x_new
move.temp[1,2] <- y_new
move.temp[1,3] <- step
move.temp[1,4] <- heading
return(move.temp)
}
Now we have a nice little function. Let’s see if it does what we want! Trial and error (or in coding parlance, debugging) represents a huge element of this process. Sometimes, we will debug within a function to make sure things are working at each step, but in this case, we have a pretty basic function, so we are going to try to run it over 100 points and see what happens. To do this, we are going to use a loop with a few parts. The first two parts are going to select the step length and turning angle from the distributions that we defined, then we are going to call the function, then we are going to add the output to one big data frame that will track all of the steps. This means that before the loop, we’ll need to create this object, which we will call steps.df:
steps.df <- data.frame(matrix(0,100,4))
colnames(steps.df) <- c("x", "y", "step.length", "turn.angle")
for (i in 2:100) {
step <- rnorm(n=1, mean=500, sd=100)
heading <- runif(n=1, min=-pi, max=pi)
next.pt <- movement(steps.df[(i-1),1:2], step, heading)
steps.df[i,] <- next.pt
}
head(steps.df)
## x y step.length turn.angle
## 1 0.0000 0.0000 0.0000 0.000000
## 2 -432.3731 322.3795 539.3283 2.500910
## 3 -612.9421 476.1830 237.1933 2.436071
## 4 -693.0755 116.1142 368.8779 4.493407
## 5 -1026.6227 518.0752 522.3279 2.263446
## 6 -1356.0456 814.0448 442.8515 2.409635
plot(steps.df$x, steps.df$y, pch=19, type='b')
points(steps.df$x[1], steps.df$y[1], pch=19, col='red', cex=1.5)
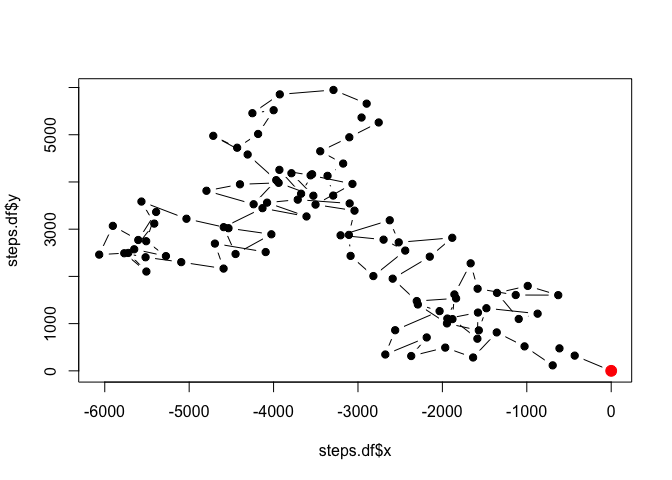
Look at that! We’ve got ourselves an output. We can see that the movement tends to be pretty random in terms of the turning angles. Every once in a while, you may have a few consecutive points that lead the animal in one direction, but these are purely stochastic, and the animal doubles back on itself with approximately the same frequency.
Now if we run the same loop again, we will not get the same results because the entire process is stochastic. The step lengths and turning angles are chosen randomly, so no two paths will really look the same. If we felt that we may need to run this loop repeatedly, perhaps because we wanted to generate 20 paths of various lengths, we could place that into a function too!
multi.move <- function(N, x) {
all.paths <- list()
for (j in 1:N) {
steps.df <- data.frame(matrix(0,100,4))
colnames(steps.df) <- c("x", "y", "step.length", "turn.angle")
for (i in 2:x[j]) {
step <- rnorm(n=1, mean=500, sd=100)
heading <- runif(n=1, min=-pi, max=pi)
next.pt <- movement(steps.df[(i-1),1:2], step, heading)
steps.df[i,] <- next.pt
}
all.paths[[j]] <- steps.df
}
return(all.paths)
}
In multi.move we allow the user to input two parameters: N (the number of individual paths they want to generate) and x of vector of length N that sets the number of points in each of the paths. Now, we return a list of N different paths, and each can have the same or different lengths; it’s all up to the user!
multi.paths <- multi.move(3, c(100,110,120))
dim(multi.paths[[2]])
## [1] 110 4
plot(multi.paths[[1]]$x, multi.paths[[1]]$y, pch=19, type='b', ylim=c(-6000,6000), xlim=c(-6000,6000))
points(multi.paths[[2]]$x, multi.paths[[2]]$y, pch=19, type='b', col='red')
points(multi.paths[[3]]$x, multi.paths[[3]]$y, pch=19, type='b', col='blue')
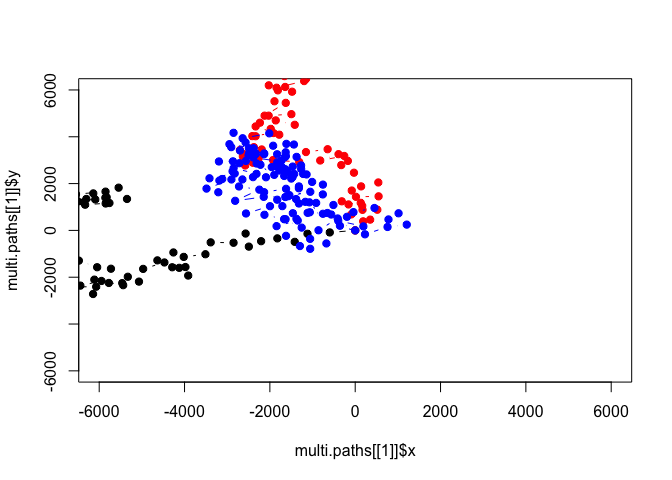
Now we can see that the second path in our new multi.paths object has 110 points because we told it to generate 110 points! How might you augment the multi.move function to allow the user to pass the starting coordinates of each individual to the function, rather than making all of them (0,0)? We can use the following points as our starting points:
N = 3
start.pts <- data.frame(matrix(0,N,2))
colnames(start.pts) <- c("x", "y")
start.pts$x <- runif(n=N, min=-500, max=500)
start.pts$y <- runif(n=N, min=-500, max=500)
Now create a multi.move2 function that uses them as the starting points of the three paths:
multi.move2 <- function(N, x, start.pts) {
all.paths <- list()
for (j in 1:N) {
steps.df <- data.frame(matrix(0,100,4))
steps.df[1,1:2] <- start.pts[j,]
colnames(steps.df) <- c("x", "y", "step.length", "turn.angle")
for (i in 2:x[j]) {
step <- rnorm(n=1, mean=500, sd=100)
heading <- runif(n=1, min=-pi, max=pi)
next.pt <- movement(steps.df[(i-1),1:2], step, heading)
steps.df[i,] <- next.pt
}
all.paths[[j]] <- steps.df
}
return(all.paths)
}