#install.packages("lme4")
library(raster)
library(lme4)
library(sf)
library(tidyverse)
library(adehabitatHR)
library(mapview)

zebra <- read_csv("data_files/Zebra_Used_LatLong_Full.csv") %>% 
  dplyr::select(ID = Name, 4:6) %>% 
  st_as_sf(., coords = 3:4, crs = "+init=epsg:4326") %>% 
  st_transform("+init=epsg:32733") %>% 
  mutate(timestamp = lubridate::mdy_hm(Date))

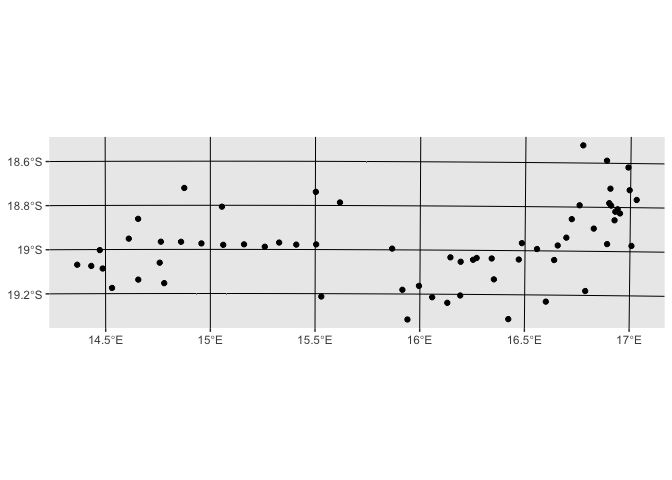
water <- st_read("data_files/ENP shapefiles/functional water.shp") %>% 
  st_transform("+init=epsg:32733")

ggplot(water) + geom_sf()

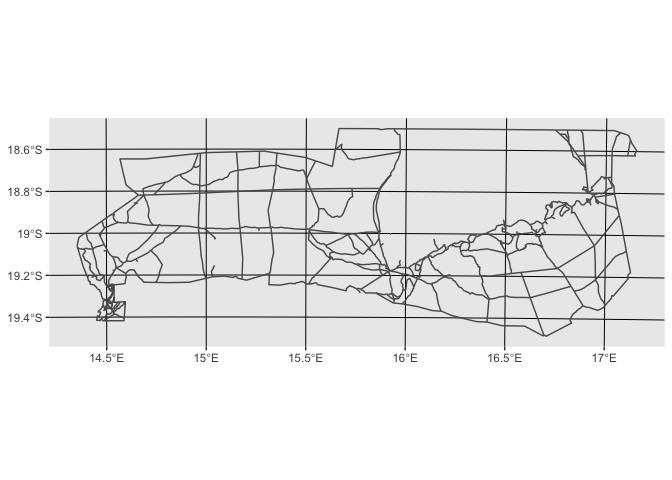
roads <- st_read("data_files/ENP shapefiles/enp roads.shp", crs = "+init=epsg:4326") %>% 
  st_transform("+init=epsg:32733")

ggplot(roads) + geom_sf()

NDVI <- raster("data_files/NDVI_200903.tif") %>% 
  projectRaster(crs="+proj=utm +zone=33 +south +datum=WGS84 +units=m +no_defs +ellps=WGS84 +towgs84=0,0,0")

# NDVI was collected in March 2009... perhaps we should limit to only the rainy season months. 
# Jan, Feb, Mar

zebra %>% 
  filter(lubridate::month(timestamp) %in% 1:3) %>% 
  sf::select.sf(-Date) %>% 
  mutate(Used = 1) -> zebra

# Choosing an available range. 
# semiconservative option - 99% UD
#zebra_ud <- adehabitatHR::kernelUD(as(zebra, "Spatial"), 
#                                   grid = 450)
zebra_ud <- adehabitatHR::kernelUD(as(zebra, "Spatial")[1],  # add the id column and you get unique homeranges
                                   grid = 450)
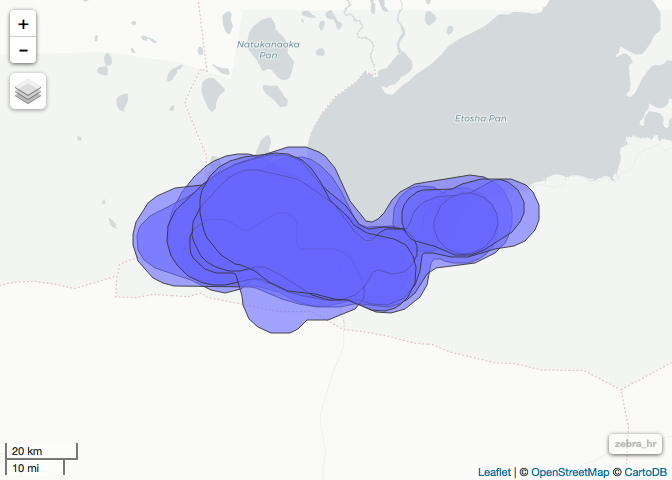
zebra_hr <- adehabitatHR::getverticeshr(zebra_ud, 99)

# let's visualize to see
homerange <- mapview(zebra_hr)
homerange

# Note a couple things here: 
# - the pan: is this really available?
# - the park fence?
# we could mask by these polygons."expert opinion"

# For now we are going to use these to sample available points. 
# First I need to know how many points to sample in each home range. 

zebra_ids <- unique(zebra$ID)
availables <- list()
for(i in 1:length(zebra_ids)){
  st_sample(st_as_sf(zebra_hr)[i,], 10*nrow(filter(zebra, ID == zebra_ids[i]))) %>% # sample individual UDs
  #st_sample(st_as_sf(zebra_hr), 10*nrow(filter(zebra, ID == zebra_ids[i])))  %>%  # 1:10 ratio; population UD
  st_sf(geometry = .) %>%
    mutate(ID = zebra_ids[i], 
          timestamp = NA, 
          Used = 0) -> availables[[i]] 
}

availables %>% 
  do.call(rbind,.) %>%
  rbind(zebra, .) -> zebra_all

head(roads)

unique(roads$TYPE)

mapview(roads, homerange)

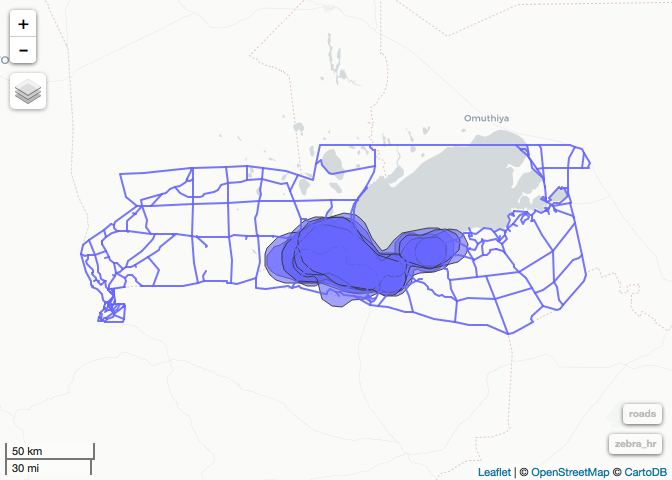
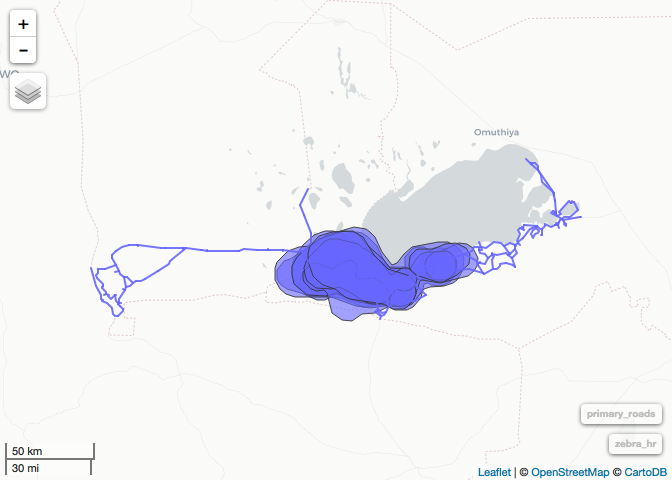
primary_roads <- filter(roads, TYPE %in% c("Tar", "Gravel"))
mapview(primary_roads, homerange)

# next step take 20 sec or so
dist<- st_distance(y=zebra_all, x=primary_roads) # a units matrix dim =[nrow(x), nrow(y)]
road_dist <- apply(dist, 2, min)
head(road_dist)

#
dist<- st_distance(y=zebra_all, x=water) # a units matrix dim =[nrow(x), nrow(y)]
water_dist <- apply(dist, 2, min)
head(water_dist)

zebra_all %>% mutate(NDVI = raster::extract(NDVI, as(., "Spatial")), 
                     dist_rd = road_dist,
                     dist_H2O = water_dist) %>% 
  group_by(ID) -> zebra_full

cor(zebra_full$NDVI, zebra_full$dist_rd)

cor(zebra_full$NDVI, zebra_full$dist_H2O)

m <- glm(Used ~ NDVI + dist_rd + dist_H2O, data=zebra_full, family=binomial(link="logit"))

stepAIC(m)

zebra_full$ID <- as_factor(zebra_full$ID)

mm <- glmer(Used ~ scale(dist_rd) + scale(dist_H2O) + (1|ID), 
           data=zebra_full, family=binomial(link="logit"))

mm

# bring in boundary of area of interest
ENP <- st_read("data_files/ENP shapefiles/enp fence poly.shp") %>% 
  st_union %>% st_transform("+init=epsg:32733")

# Let's match the resolution of our NDVI layer
# res(NDVI)

# make a grid and calculate distances
enp_grid <- st_make_grid(ENP, n = c(1266, 476), what= "centers") 
# convert to raster
dist_raster <- raster(as(enp_grid, "Spatial"), ncol=1266, nrow= 476)

# dist_road_grid <- st_distance(primary_roads, enp_grid)
dist_water_grid <- st_distance(water, enp_grid)
# dist_raster[] = apply(dist_road_grid, 2, min)
dist_raster[] = apply(dist_water_grid, 2, min)


plot(dist_raster)
plot(st_geometry(water), add=TRUE)

# alternative method using sp and regos libraries -- comparable, doesn't require flip
#require(rgeos)
#dd = gDistance(as(water, "Spatial"), as(dist_raster,"SpatialPoints"), byid=TRUE)
#dist_raster[] = apply(dd,1,min)

dist_road <- raster("data_files/Dist_PrimaryRoads.tif") %>% flip(2)
dist_water <- raster("data_files/Dist_Water.tif") %>% flip(2)

# why are we using flip?
# these files were created with st_distance function. gDistance would not require this. 
# http://rspatial.org/spatial/rst/8-rastermanip.html
# "flip lets you flip the data (reverse order) in horizontal or vertical direction – typically to correct for a ‘communication problem’ between different R packages or a misinterpreted file."
# sf and raster have a "communication problem", in the way the distance is calculated in st_distance. 



# make a dataframe of all variable points:
# step 1 make ndvi points match in space to the dist variables
ndvi <- resample(crop(NDVI, extent(dist_road)), dist_road)
# stack them all
rasters <- stack(ndvi, dist_road, dist_water)
names(rasters) <- c("NDVI", "dist_rd", "dist_H2O")

#predictions based on best model
best_m <- glm(Used ~ dist_rd + dist_H2O, data=zebra_full, family=binomial(link="logit"))

# make a predicted raster layer based upon glm
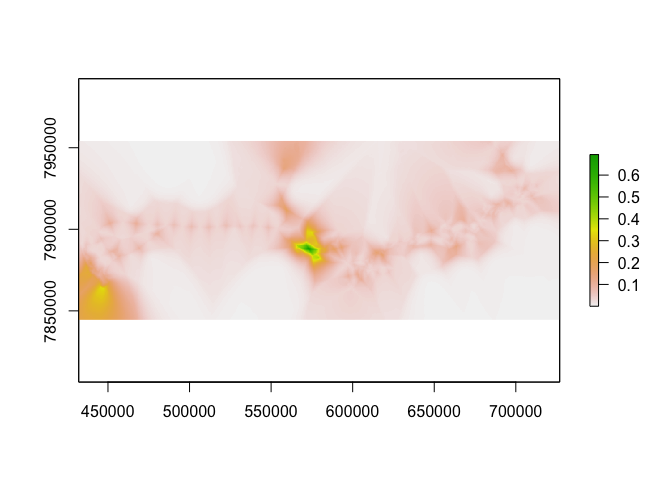
predictions = raster::predict(object = rasters, model=m, fun=predict)
predictions = exp(predictions)

plot(predictions)