library(tlocoh)
## Loading required package: sp
## T-LoCoH for R (version 1.40.04)
## URL: http://tlocoh.r-forge.r-project.org/
## Bug reports: tlocoh@gmail.com
load('toni.n5775.lxy.01.RData')
load('toni.n5775.s0.k15.iso.lhs.01.RData')
We have seen how to create a LoCoH-based utilization distribution that depends entirely on the spatial proximity of positional fixes, but now let’s think about incorporating the temporal component to our analysis. As we saw in that first plot of our track, the animal definitely used the same space at different times. The current lhs object that we created ignored the separation of these points in time and creates a hull out of the nearest points in terms of spatial proximity alone. But knowing what we do, we should really consider time and at least examine how things change.
We are going to return to our lxy object (which already has one set of nearest neighbors attached), and create a new nearest neighbor set with a non-zero s parameter. But we don’t want to select this value willy-nilly! Fortunately, Andy has a few different methods that we can use to obtain a reasonable s value. The first is to pick an s value such that 40-80% of the hulls are ‘time-selected.’ All you need to do for this method is use the tlocoh::lxy.ptsh.add command:
toni.lxy <- lxy.ptsh.add(toni.lxy)
## id: toni
## Randomly selected 200 of 5775 points
## Finding 10 nearest neighbors for 200 sample points
## Finding s for ptsh=0.98
## s=0.005, s=0.01, s=0.02, s=0.04, s=0.08, s=0.16,
## Finding s for ptsh=0.1 (+/- 0.01)
## s=0.0025, s=0.00125, s=0.000625, s=0.0003125, s=0.00015625,
## s=0.000234375, s=0.0001953125, s=0.00017578125,
## Finding s for ptsh=0.2 (+/- 0.01)
## Finding s for ptsh=0.3 (+/- 0.01)
## Finding s for ptsh=0.4 (+/- 0.01)
## s=0.0075,
## Finding s for ptsh=0.5 (+/- 0.01)
## s=0.015, s=0.0125, s=0.01125, s=0.011875,
## Finding s for ptsh=0.6 (+/- 0.01)
## s=0.0175, s=0.01625,
## Finding s for ptsh=0.7 (+/- 0.01)
## s=0.03, s=0.025, s=0.0225,
## Finding s for ptsh=0.8 (+/- 0.01)
## Finding s for ptsh=0.9 (+/- 0.01)
## s=0.06, s=0.05, s=0.045,
##
## Done with toni
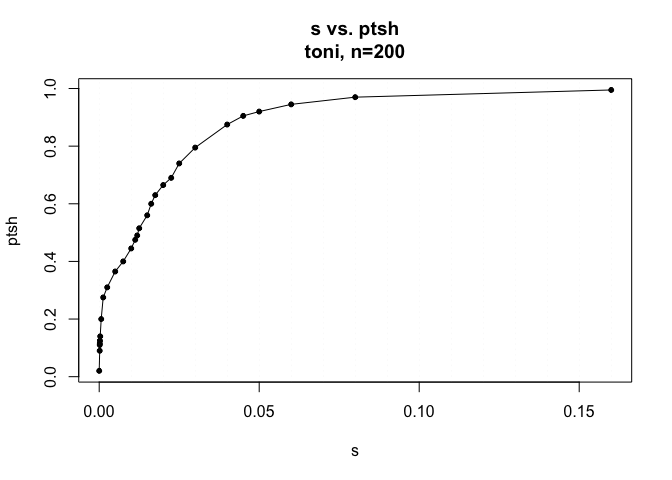
This creates a set of 200 sample points, each with 10 nearest neighbors. This algorithm goes through a set of different s values and determines what proportion of hulls are time-selected. Though this is a somewhat stochastic process, we can see that s values between approximiately 0.01 and 0.035 fall between proportions of time-selected hulls ranging from about 40-80%. For simplicity, there is also a nice plot that shows the change in the proportion of time selected hulls over various s values to find an optimal point. It seems like 0.03 is a reasonable choice.
The second method is a little more involved. First we need to select a time interval of interest, which will be based on the temporal scale of the question we are asking. For example, we may be interested in daily foraging patterns. If that is the case, we may not want to treat points that occur more than 24 hours apart in time as nearest neighbors of one another, even if they occur close in space. If we are thinking about seasonal patterns, however, points that occur several weeks apart may still reasonably be considered nearest neighbors. If you are unsure exactly what time interval you are most interested in, you can use the tlocoh::lxy.plot.pt2ctr command which plots the distance of each point to the centroid of the entire dataset. This may help isolate the ‘natural’ frequencies in the data.
lxy.plot.pt2ctr(toni.lxy)
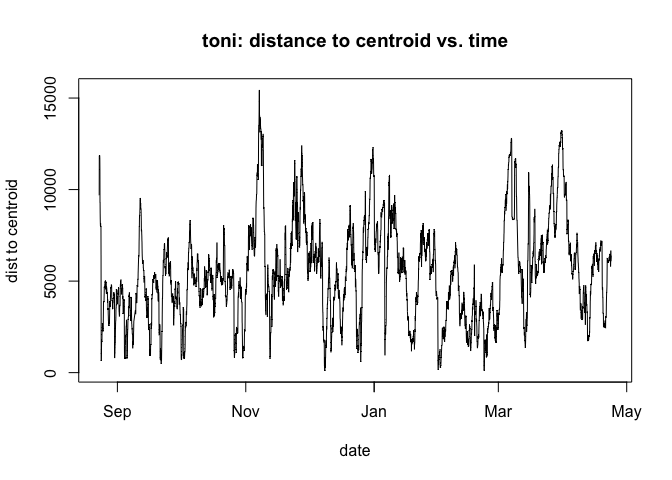
Looking at that, it is a little difficult to pick out especially notable patterns, but depending on your data, something may jump out. Even without using that, we can call the `tlocoh::lxy.plot.sfinder command:
lxy.plot.sfinder(toni.lxy)
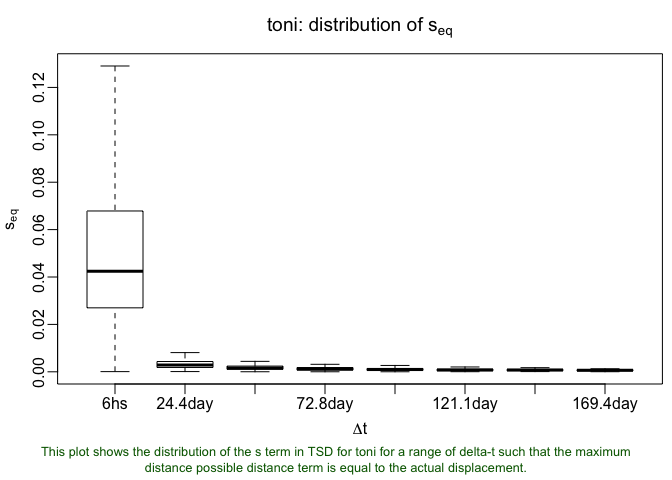
This shows that approximately half of all pairs of points will be time-selected at the scale of 24 hours when s is somewhere around 0.005 to 0.01. We can get a closer look by defining a specific set of delta.t values:
lxy.plot.sfinder(toni.lxy, delta.t=3600*c(12,24,36,48,54,60))
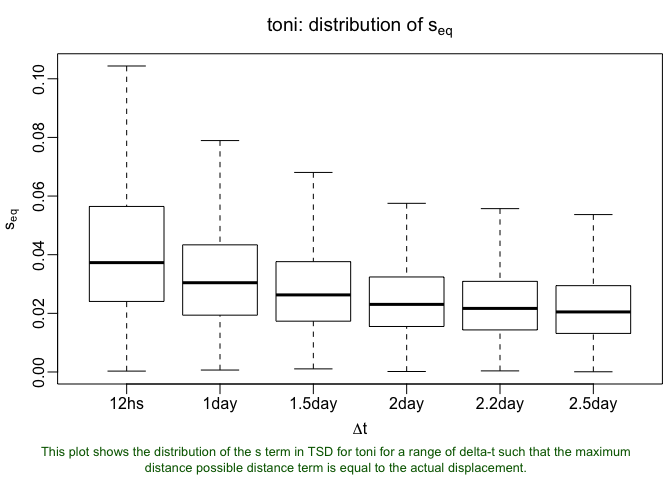
That’s better! It looks like the results here support the use of 0.03 as our s value. It would not be especially surprising if the two methods did not converge on a single s value, though. They are approaching the selection of s in very different ways. The fact of the matter is that there is not perfect s value. Changes in that parameter will result in different hullsets that tell us different things. Fortunately, we’ve landed on a value of 0.03 using both methods!
Now that we have an s value chosen, let’s return to our lxy object and create a new set of nearest neighbors. We will use the same k value of 25, but we’ll set an s value this time:
toni.lxy <- lxy.nn.add(toni.lxy, s=0.03, k=25)
## Finding nearest neighbors for id=toni (n=5775),
## num.parent.pts=5775, mode=Fixed-k, k=25, s=0.03, method=TSD:vmax
## - computing values of kmax, rmax, and amax...Done
## - set of neighbors (re)named: toni|vmax|s0.03|n5775|kmax25|rmax1301.9|amax17017.7
##
## Done. Nearest neighbor set(s) created / updated:
## toni|vmax|s0.03|n5775|kmax25|rmax1301.9|amax17017.7
## Total time: 42 secs
This simply adds another nearest neighbor set, which we can see if we use the tlocoh:summary function again:
summary(toni.lxy)
## Summary of LoCoH-xy object: toni.lxy
## ***Locations
## id num.pts dups
## toni 5775 9
## ***Time span
## id begin end period
## toni 2005-08-23 2006-04-23 243.3 days
## ***Spatial extent
## x: 369305.5 - 391823.9
## y: 7305737.9 - 7330491.3
## proj: +proj=utm +south +zone=36 +ellps=WGS84
## ***Movement properties
## id time.step.median d.bar vmax
## toni 3600 (1hs) 173.7452 0.9267969
## ***Ancilliary Variables:
## -none-
## ***ptsh s-values computed
## id k n ptsh
## toni 10 200 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9,
## 0.98
## ***Nearest-neighbor set(s):
## 1 toni|vmax|s0|n5775|kmax25|rmax57.8|amax701
## 2 toni|vmax|s0.03|n5775|kmax25|rmax1301.9|amax17017.7
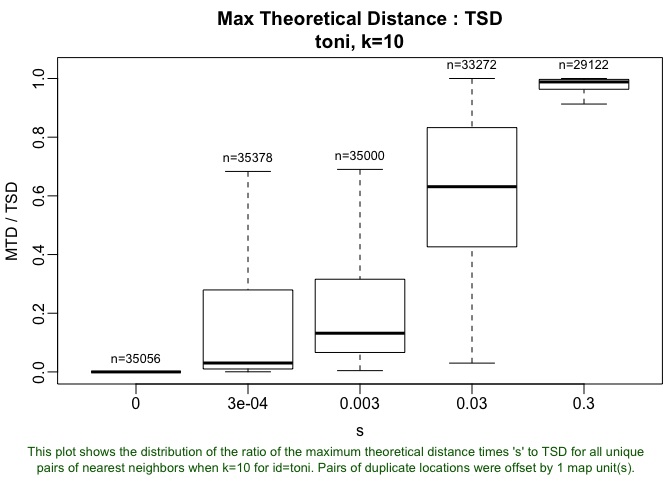
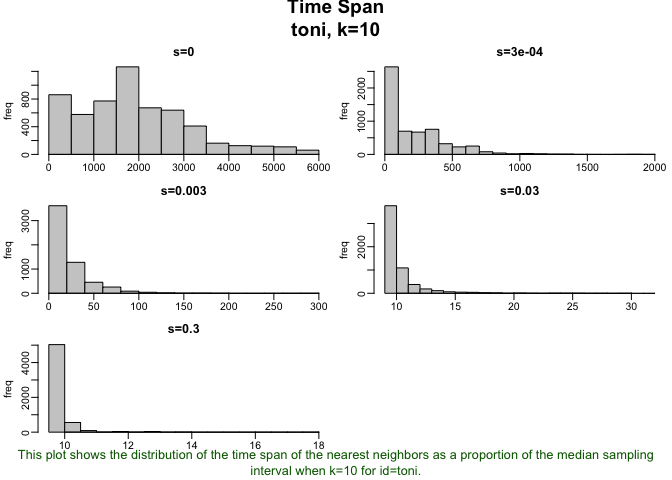
Now there are two items under the nearest neighbor sets! Mission accomplished. We could also have gone about selecting s in a similar fashion as we selected k, essentially creating a set of alternative nearest neighbor sets and comparing the emergent properties of each. In this case, we might want to use the tlocoh::lxy.plot.mtdr command to examine the ratios of diffusion distance to time-scaled distance or tlocoh::lxy.plot.tspan to see the time spans of the resulting hulls.
toni.lxy <- lxy.nn.add(toni.lxy, s=c(0.0003, 0.003, 0.03, 0.3), k=25)
## Finding nearest neighbors for id=toni (n=5775),
## num.parent.pts=5775, mode=Fixed-k, k=25, s=3e-04,
## method=TSD:vmax
## - computing values of kmax, rmax, and amax...Done
## - set of neighbors (re)named: toni|vmax|s3e-04|n5775|kmax25|rmax162.9|amax1399.3
## Finding nearest neighbors for id=toni (n=5775),
## num.parent.pts=5775, mode=Fixed-k, k=25, s=0.003,
## method=TSD:vmax
## - computing values of kmax, rmax, and amax...Done
## - set of neighbors (re)named: toni|vmax|s0.003|n5775|kmax25|rmax222.8|amax2349.7
## Finding nearest neighbors for id=toni (n=5775),
## num.parent.pts=5775, mode=Fixed-k, k=25, s=0.03, method=TSD:vmax
## - there is already a set of nearest neighbors for this set of
## parent points and value of s.
## - enough points already saved, no need to find more
## Finding nearest neighbors for id=toni (n=5775),
## num.parent.pts=5775, mode=Fixed-k, k=25, s=0.3, method=TSD:vmax
## - computing values of kmax, rmax, and amax...Done
## - set of neighbors (re)named: toni|vmax|s0.3|n5775|kmax25|rmax12947.9|amax169162.3
##
## Done. Nearest neighbor set(s) created / updated:
## toni|vmax|s3e-04|n5775|kmax25|rmax162.9|amax1399.3
## toni|vmax|s0.003|n5775|kmax25|rmax222.8|amax2349.7
## toni|vmax|s0.3|n5775|kmax25|rmax12947.9|amax169162.3
## Total time: 1.6 mins
lxy.plot.mtdr(toni.lxy, k=10)
## Computing maximum theoretical distance over TSD for toni
##
|
| | 0%
|
|============= | 20%
|
|========================== | 40%
|
|======================================= | 60%
|
|==================================================== | 80%
|
|=================================================================| 100%
lxy.plot.tspan(toni.lxy, k=10)
## Computing time span for toni
##
|
| | 0%
|
|============= | 20%
|
|========================== | 40%
|
|======================================= | 60%
|
|==================================================== | 80%
|
|=================================================================| 100%
These methods still leave a great deal up to the researcher, which has its pros and cons, but at least you’ve got quite a few alternatives for selecting an ideal s value for your particular purposes. We’ll stick with our 0.03 value for now, but we’ll need to create a new lhs object using this parameter:
toni.lhs.time <- lxy.lhs(toni.lxy, k=3*3:8, s=0.03)
## Using nearest-neighbor selection mode: Fixed-k
## Constructing hulls and hull metrics...
## toni: 9 duplicate points were randomly displaced by 1 map unit(s)
##
## toni.pts5775.k9.s0.03.kmin0
## Found a suitable set of nearest neighbors
## Identifying the boundary points for each parent point
## Converting boundary points into polygons
## Calculating area and perimeter...Done.
## Calculating the time span of each hull...Done.
## Identifying enclosed points...Done.
##
## toni.pts5775.k12.s0.03.kmin0
## Found a suitable set of nearest neighbors
## Identifying the boundary points for each parent point
## Converting boundary points into polygons
## Calculating area and perimeter...Done.
## Calculating the time span of each hull...Done.
## Identifying enclosed points...Done.
##
## toni.pts5775.k15.s0.03.kmin0
## Found a suitable set of nearest neighbors
## Identifying the boundary points for each parent point
## Converting boundary points into polygons
## Calculating area and perimeter...Done.
## Calculating the time span of each hull...Done.
## Identifying enclosed points...Done.
##
## toni.pts5775.k18.s0.03.kmin0
## Found a suitable set of nearest neighbors
## Identifying the boundary points for each parent point
## Converting boundary points into polygons
## Calculating area and perimeter...Done.
## Calculating the time span of each hull...Done.
## Identifying enclosed points...Done.
##
## toni.pts5775.k21.s0.03.kmin0
## Found a suitable set of nearest neighbors
## Identifying the boundary points for each parent point
## Converting boundary points into polygons
## Calculating area and perimeter...Done.
## Calculating the time span of each hull...Done.
## Identifying enclosed points...Done.
##
## toni.pts5775.k24.s0.03.kmin0
## Found a suitable set of nearest neighbors
## Identifying the boundary points for each parent point
## Converting boundary points into polygons
## Calculating area and perimeter...Done.
## Calculating the time span of each hull...Done.
## Identifying enclosed points...Done.
## The following hullsets were generated:
## toni.pts5775.k9.s0.03.kmin0
## toni.pts5775.k12.s0.03.kmin0
## toni.pts5775.k15.s0.03.kmin0
## toni.pts5775.k18.s0.03.kmin0
## toni.pts5775.k21.s0.03.kmin0
## toni.pts5775.k24.s0.03.kmin0
## Total time: 17.3 secs
toni.lhs.time <- lhs.iso.add(toni.lhs.time)
## Merging hulls into isopleths
## toni.pts5775.k9.s0.03.kmin0
## Sorting hulls by area...Done.
## Unioning hulls
##
|
| | 0%
|
|++++++++++ | 20%
|
|++++++++++++++++++++ | 40%
|
|+++++++++++++++++++++++++++++ | 60%
|
|+++++++++++++++++++++++++++++++++++++++ | 80%
|
|+++++++++++++++++++++++++++++++++++++++++++++++++| 100%
## toni.pts5775.k12.s0.03.kmin0
## Sorting hulls by area...Done.
## Unioning hulls
##
|
| | 0%
|
|++++++++++ | 20%
|
|++++++++++++++++++++ | 40%
|
|+++++++++++++++++++++++++++++ | 60%
|
|+++++++++++++++++++++++++++++++++++++++ | 80%
|
|+++++++++++++++++++++++++++++++++++++++++++++++++| 100%
## toni.pts5775.k15.s0.03.kmin0
## Sorting hulls by area...Done.
## Unioning hulls
##
|
| | 0%
|
|++++++++++ | 20%
|
|++++++++++++++++++++ | 40%
|
|+++++++++++++++++++++++++++++ | 60%
|
|+++++++++++++++++++++++++++++++++++++++ | 80%
|
|+++++++++++++++++++++++++++++++++++++++++++++++++| 100%
## toni.pts5775.k18.s0.03.kmin0
## Sorting hulls by area...Done.
## Unioning hulls
##
|
| | 0%
|
|++++++++++ | 20%
|
|++++++++++++++++++++ | 40%
|
|+++++++++++++++++++++++++++++ | 60%
|
|+++++++++++++++++++++++++++++++++++++++ | 80%
|
|+++++++++++++++++++++++++++++++++++++++++++++++++| 100%
## toni.pts5775.k21.s0.03.kmin0
## Sorting hulls by area...Done.
## Unioning hulls
##
|
| | 0%
|
|++++++++++ | 20%
|
|++++++++++++++++++++ | 40%
|
|+++++++++++++++++++++++++++++ | 60%
|
|+++++++++++++++++++++++++++++++++++++++ | 80%
|
|+++++++++++++++++++++++++++++++++++++++++++++++++| 100%
## toni.pts5775.k24.s0.03.kmin0
## Sorting hulls by area...Done.
## Unioning hulls
##
|
| | 0%
|
|++++++++++ | 20%
|
|++++++++++++++++++++ | 40%
|
|+++++++++++++++++++++++++++++ | 60%
|
|+++++++++++++++++++++++++++++++++++++++ | 80%
|
|+++++++++++++++++++++++++++++++++++++++++++++++++| 100%
## Total time: 8.4 secs
plot(toni.lhs.time, iso=TRUE, figs.per.page=6)
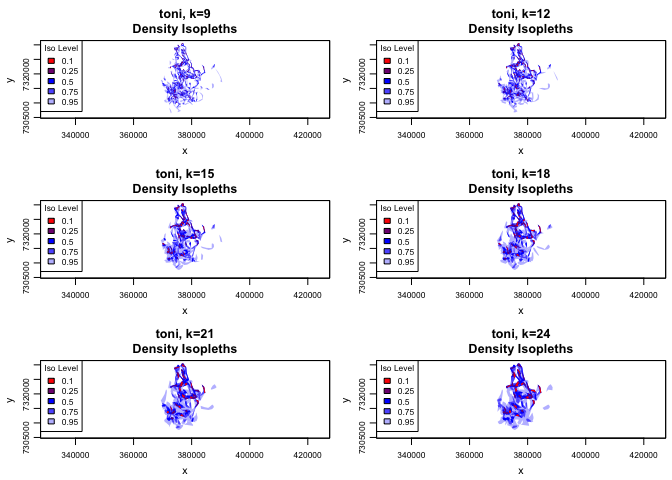
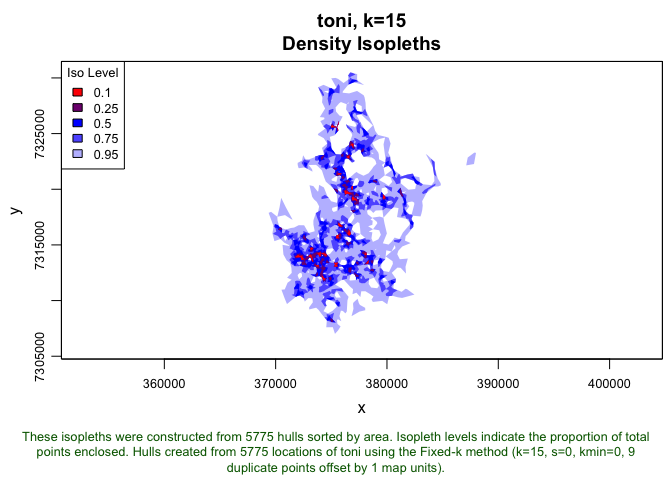
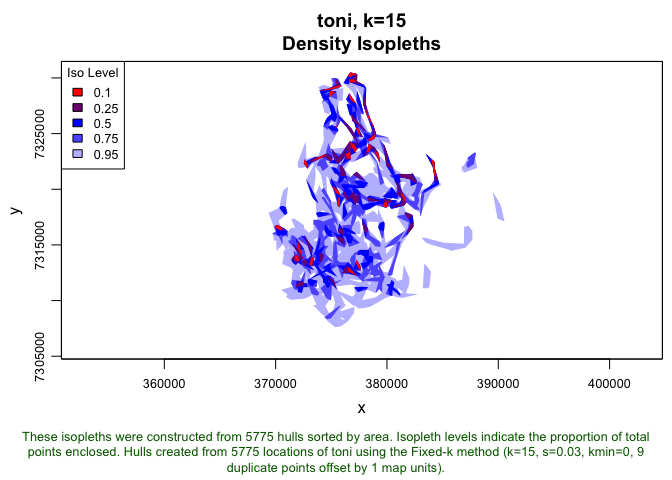
Once again, it looks like k=15 meets the eyeball-test, even when we incorporate the temporal component. We can take one last look to see what the old isopleths (without time) look like in comparison to these (with time).
toni.lhs.time.k15 <- lhs.select(toni.lhs.time, k=15)
plot(toni.lhs.k15, iso=TRUE, figs.per.page=1)
plot(toni.lhs.time.k15, iso=TRUE, figs.per.page=1)
Before we finish up this segment, let’s make sure we save our new hullset so that we can use it in the next lesson!
lhs.save(toni.lhs.time.k15)
## LoCoH-hullset toni.lhs.time.k15 saved as 'toni.lhs.time.k15' to:
## /Users/dseidel/Desktop/HongKong/Materials/Day4/toni.n5775.s0.03.k15.iso.lhs.02.RData
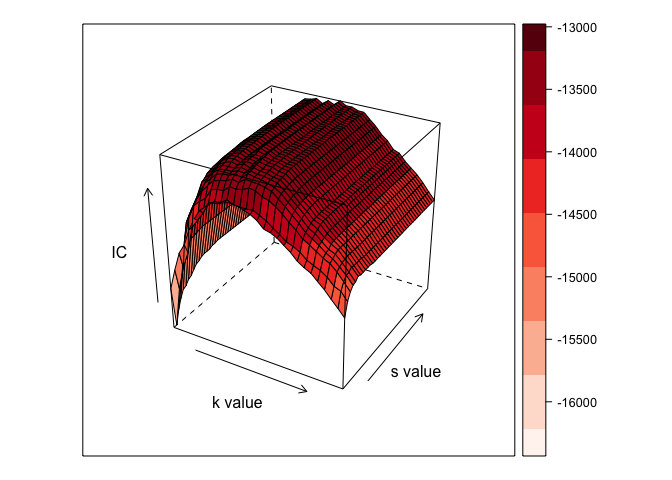
One final bit of information regarding the parameter seletion process. I am sure you have noticed that there is quite a lot of subjectivity in all of the methods we went over for selecting s and k. Though this offers a great deal of flexibility (one of the stengths of the T-LoCoH algorithm and package), it makes many researchers a bit uncomfortable. In order to circumvent some of this discomfort, several of my colleagues and I proposed an alternative method for simultaneously selecting appropriate s and k values using a grid-based search and an information criterion of our devising. Though this takes longer than the alternatives mentioned above, it does offer a fundamental theoretical underpinning to the selection process. Below is a function that wraps up this search process and outputs a data frame with values based on two different information criteria (one siliar to AIC and another akin to BIC). Let’s go through the code together, and based on what we have done above, we’ll try to figure out what this algorithm does to optimize the two parameters.
The first function train.test doesn’t actually depend on T-LoCoH at all. We are just creating a set of 100 different training/testing data sets for use in the algo function. This is where we actually create hullsets and attempt to determine the optimal parameter values. The inputs are the training/testing set we made in the previous function, a vector of the k values we want to search over, a single value for the number of different s values to test for (i.e., 40 will result in divisions of 0.025 each), the lxy object, and finally, the original dataset.
train.test <- function (data, seed) {
df <- data.frame(matrix(TRUE,nrow(data),100))
set.seed(seed)
for (i in 1:ncol(df)) {
samp <- sample(seq(1,nrow(data),1), round(0.002222*(nrow(data))))
for (j in 1:length(samp)) {
for (k in 1:nrow(df)) {
if (k == samp[j]) {
df[k,i] <- FALSE
}
}
}
}
count <- 0
for (i in 1:ncol(df)) {
new <- table(df[,i])[1]
count <- count + new
}
for (i in 3:nrow(df)) {
for (j in 1:ncol(df)) {
if (df[i-1,j] == FALSE && df[i-2,j] != FALSE) {
for (k in 0:98) {
df[i+k,j] <- FALSE
}
}
}
}
df <- df[1:nrow(data),]
return(df)
}
algo <- function(train.test, k.vals, s.max, num.s.vals, data.lxy, data) {
# Determine number of test points across all 100 train/test splits for BIC calculation
count <- 0
for (i in 1:ncol(train.test)) {
new <- table(train.test[,i])[1]
count <- count + new
}
trace <- data.frame(matrix(0,length(k.vals),7))
for (k in 1:length(k.vals)) {
for (z in 1:(num.s.vals + 1)) {
current.k_val <- k.vals[k]
current.s_val <- (z-1) * (s.max/num.s.vals)
# Calculate the nearest neighbors and create lhs object for full dataset
full.lxy <- lxy.nn.add(data.lxy, k=current.k_val, s=current.s_val, status=F)
full.lhs <- lxy.lhs(full.lxy, k=current.k_val, s=current.s_val, status=F)
coords <- full.lhs[[1]]$pts@coords
# Create list for the negative log likelihood values for each test/train split in df
likelihood <- list()
for (j in 1:ncol(train.test)) {
# Create a one-column data frame from df
df1 <- train.test[1:nrow(train.test),j]
# Create selection of hulls based on Boolean
hulls.sel.idx <- which(df1)
full.hulls <- hulls(full.lhs)
selected.hulls <- full.hulls[[1]] [ full.hulls[[1]]@data$pts.idx %in% hulls.sel.idx , ]
# Determine the number of points in training dataset
df.temp <- data.frame(as.numeric(train.test[,j]))
colnames(df.temp) <- "subset"
total.pts <- sum(df.temp)
# Find middle points of testing data and define as -1
for (i in 2:nrow(df.temp)) {
if (df.temp[i,1] == 0 && df.temp[i-1,1] != 0 && df.temp[i-1,1] != -1) {
df.temp[i+50,1] <- -1
}
}
df.temp <- df.temp[1:nrow(data),]
df.temp <- cbind(coords, df.temp)
# Extract the middle points for testing and record associated coordinates
test.pts <- data.frame()
q = 1
for (i in 1:nrow(df.temp)) {
if (df.temp[i,3] == -1) {
test.pts[q,1] <- df.temp[i,1]
test.pts[q,2] <- df.temp[i,2]
q = q + 1
}
}
colnames(test.pts) <- c("x", "y")
test.pts <- SpatialPoints(test.pts[ , c("x","y")], proj4string=CRS("+proj=utm +south +zone=35 +ellps=WGS84"))
poly <- SpatialPolygons(selected.hulls@polygons, proj4string = CRS('+proj=utm +south +zone=35 +ellps=WGS84'))
# Determine the number of hulls under each test point,
overlay <- data.frame(matrix(0,length(test.pts@coords[,1]),1))
for (i in 1:length(test.pts@coords[,1])) {
overlay.list <- over(test.pts[i], poly, returnList=TRUE)
overlay[i,1] <- length(overlay.list[[1]])
}
hull.mean <- mean(full.lhs[[1]]$hulls@data$area)
# Calculate likelihood
for (i in 1:nrow(overlay)) {
overlay[i,2] <- overlay[i,1]/length(selected.hulls[[1]])
overlay[i,3] <- -log(overlay[i,2])
overlay[i,4] <- log(overlay[i,2],exp(1))
if (overlay[i,1] == 0) {
overlay[i,3] <- -log((1/nrow(data))/100)
overlay[i,4] <- log((1/nrow(data))/100, exp(1))
overlay[i,4] <- log((1/nrow(data))/100, exp(1))
}
}
colnames(overlay) <- c("over", "prob", "loglike", "ln.like")
# Add values to likelihood list
likelihood[[j]] <- as.list(overlay)
}
log.like <- data.frame(matrix(0,length(likelihood),4))
for (i in 1:length(likelihood)) {
log.like[i,1] <- sum(likelihood[[i]]$loglike, na.rm=TRUE)
log.like[i,2] <- sum(likelihood[[i]]$ln.like, na.rm=TRUE)
log.like[i,3] <- -2*(log.like[i,2]) + 2*k
log.like[i,4] <- -2*(log.like[i,2]) + k*log(as.numeric(count),exp(1))
}
# Assign mean of the means of negative log likelihoods as the current posterior probability for Metropolis-Hastings
new.postLike <- sum(log.like[,1])
new.lnLike <- sum(log.like[,2])
new.AIC <- sum(log.like[,3])
new.BIC <- sum(log.like[,4])
#cat("iteration:", counter, "chain:", current.k_val, current.s_val, "likelihood:", new.postLike, "\n")
trace[((k-1)*(num.s.vals+1))+z,1] <- current.s_val
trace[((k-1)*(num.s.vals+1))+z,2] <- current.k_val
trace[((k-1)*(num.s.vals+1))+z,3] <- hull.mean
trace[((k-1)*(num.s.vals+1))+z,4] <- new.postLike
trace[((k-1)*(num.s.vals+1))+z,5] <- new.lnLike
trace[((k-1)*(num.s.vals+1))+z,6] <- new.AIC
trace[((k-1)*(num.s.vals+1))+z,7] <- new.BIC
colnames(trace) <- c("s.val", "k.val", "hull.mean", "postLike", "lnLike", "AIC", "BIC")
} # End of s loop
} # End of k loop
return(trace)
}
Just to show what the result would look like without going through the multi-hour computation, we can call in an existing trace output:
trace <- read.csv('Example_Trace.csv')
#install.packages('lattice')
library(lattice)
my.palette <- c("#FFF5F0", "#FEE0D2", "#FEE0D2", "#FCBBA1", "#FCBBA1", "#FC9272", "#FC9272", "#FB6A4A", "#FB6A4A", "#EF3B2C", "#EF3B2C", "#CB181D", "#CB181D", "#A50F15", "#A50F15", "#67000D")
levelplot(-trace$X7 ~ trace$X2 * trace$X3, xlab="k value", ylab="s value", zlab="IC", screen = list(z = -30, x=-60), regions=TRUE, cuts=15, col.regions=my.palette)
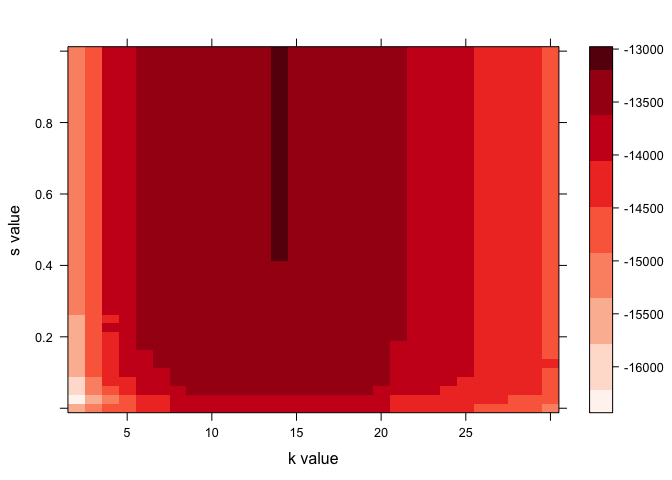
wireframe(-trace$X7 ~ trace$X2 * trace$X3, xlab="k value", ylab="s value", zlab="IC", screen = list(z = -30, x=-60), drape=TRUE, cuts=15, col.regions=my.palette)